Freshservice : Simplified ITSM Powered by AI

Freshservice: in summary
Freshservice is a cloud-based ITSM (IT Service Management) solution designed to simplify service management within organizations. It’s built for IT teams as well as HR, facilities, legal, or finance departments in medium to large organizations that require structured, efficient, and collaborative support. Freshservice follows ITIL best practices while remaining easy to deploy and manage.
With intelligent automation, unified asset and service management, and advanced AI capabilities (Freddy Copilot), Freshservice reduces repetitive tasks, improves agent productivity, and speeds up issue resolution. It also enables smooth cross-functional workflows and a better employee experience.
What are the main features of Freshservice?
Incident and Problem Management
Freshservice helps teams capture, track, and resolve incidents efficiently. Tickets are automatically sorted, assigned, and prioritized based on severity, which shortens resolution times and improves service quality.
- Automated ticket routing
- Standardized responses using templates
- Full incident history to identify root causes
- Enhanced collaboration through the service portal
Change Management
This feature allows for planning, tracking, and executing technical changes with strict control to minimize risk and ensure service continuity.
- Configurable change types (standard, normal, urgent)
- Automated approval workflows
- Complete audit logging
- Integration with asset and CMDB modules
IT Asset Management (ITAM)
Freshservice provides full asset lifecycle management—from deployment to retirement. It enables teams to track devices, software, licenses, and contracts.
- Automatic discovery via agent-based or agentless methods
- Software compliance tracking
- Centralized management of purchases and contracts
- Vendor integration for hardware updates
Configuration Management Database (CMDB)
The CMDB shows the relationships between services, assets, incidents, and users to support informed decision-making.
- Dependency mapping of technical components
- Impact analysis before changes
- Sync with automatically collected data
- Centralized configuration object management
Self-Service Portal and Knowledge Base
Freshservice provides an intuitive self-service portal where employees can access help articles, submit requests, or check the status of existing tickets.
- Smart search with automatic suggestions
- Access to FAQs and step-by-step guides
- Reduced ticket volume through self-resolution
- Customizable portals by team or department
Intelligent Automation with Freddy Copilot
Freddy, the built-in AI assistant, supports agents by automating repetitive tasks, generating responses, and predicting user needs.
- Contextual suggestions in tickets
- Automatic drafting of replies
- Predictive analysis of incident trends
- Cross-application process automation
Service Orchestration
Freshservice connects tools and workflows to automate organization-wide business processes, such as employee onboarding, access provisioning, or HR requests.
- Integrations with Active Directory, Microsoft 365, Jira, Slack, Zoom, and more
- Event triggers and automation rules
- No-code creation of complex workflows
- Centralized monitoring of task execution
Why choose Freshservice?
- Fast deployment and easy adoption – Intuitive interface, guided setup, and rapid go-live.
- Native automation across the service lifecycle – Reduces manual work and optimizes workflows.
- Improved employee experience – Simple, accessible portal for all departments.
- Integrated, proactive AI – Freddy Copilot anticipates, assists, and continuously improves outcomes.
- Modular approach for all teams – Independent configuration for IT, HR, legal, facilities, and more.
Its benefits
Extensive no-code automation
Built-in AI with Freddy Copilot
Unified management of services and assets
Customizable self-service portal
Quick deployment and intuitive usability
GDPR
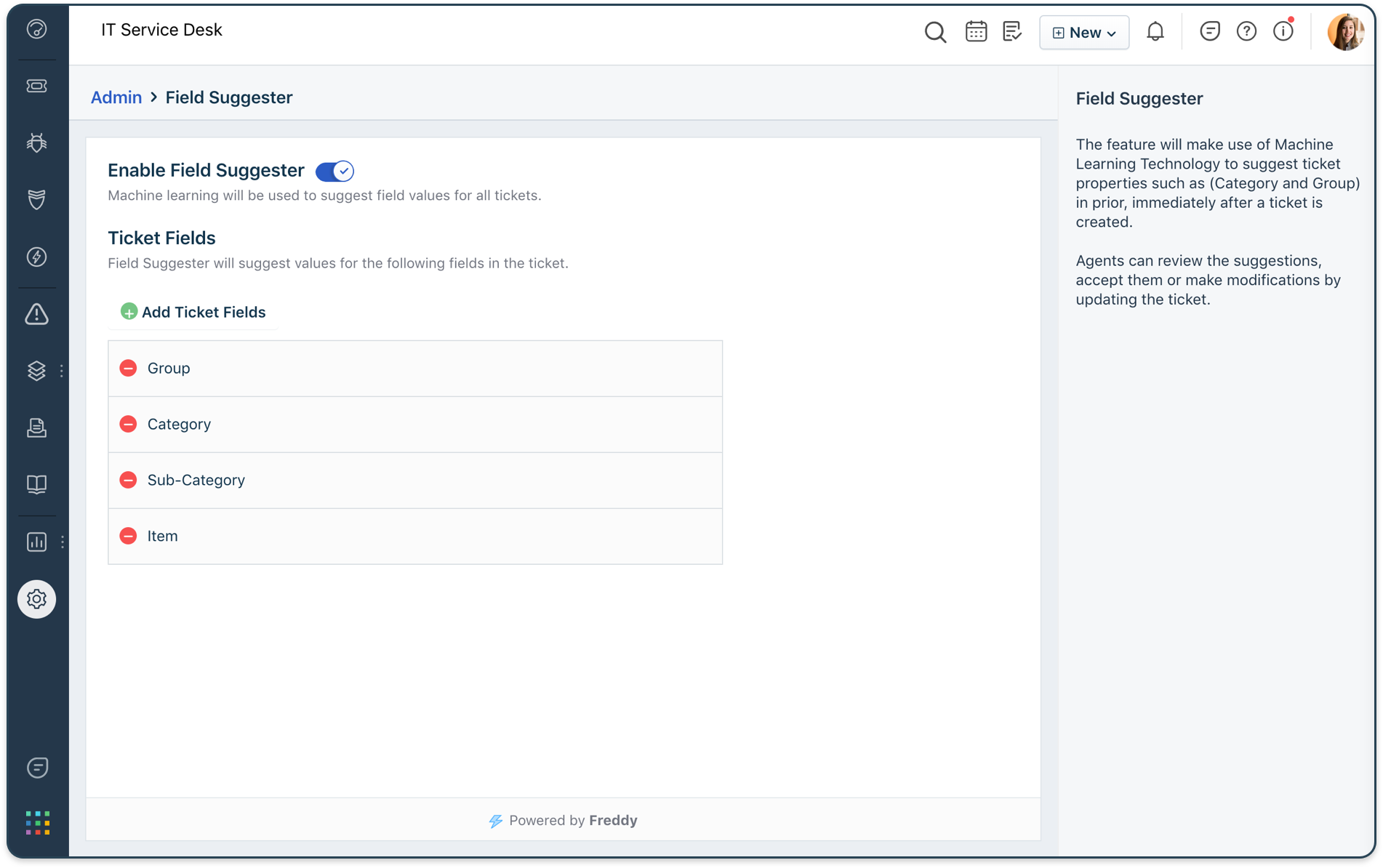 Freshservice - Improve agent productivity by triaging incoming tickets and providing ML-powered suggestions and responses,
Freshservice - Improve agent productivity by triaging incoming tickets and providing ML-powered suggestions and responses, 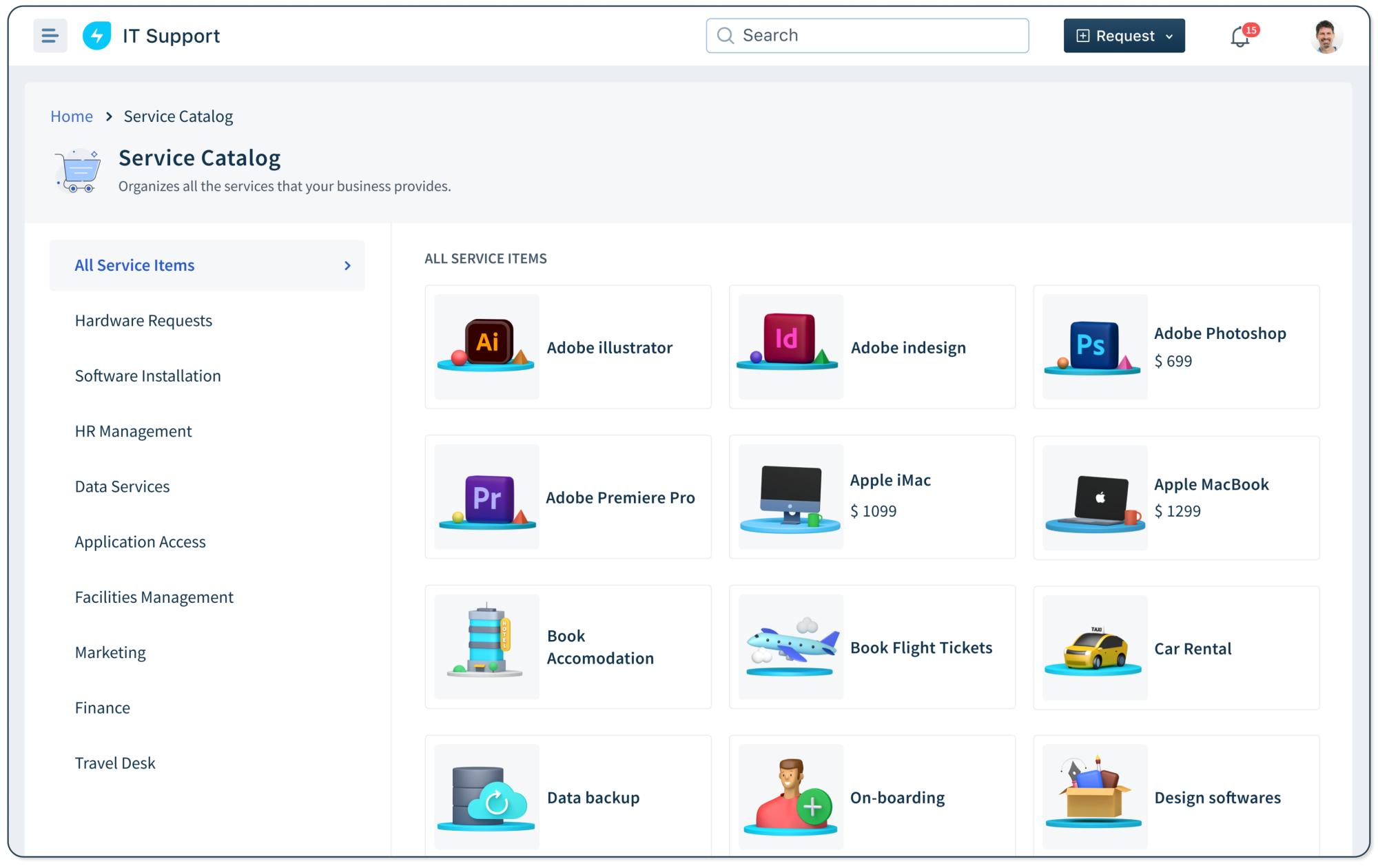 Freshservice - Streamline service management across lines of business, from IT to HR, Facilities, Travel, Legal, and more.
Freshservice - Streamline service management across lines of business, from IT to HR, Facilities, Travel, Legal, and more.  Freshservice - Meet your expanding customer needs with the open and flexible Freshworks Platform providing rich API for custom integrations and an apps marketplace.
Freshservice - Meet your expanding customer needs with the open and flexible Freshworks Platform providing rich API for custom integrations and an apps marketplace. 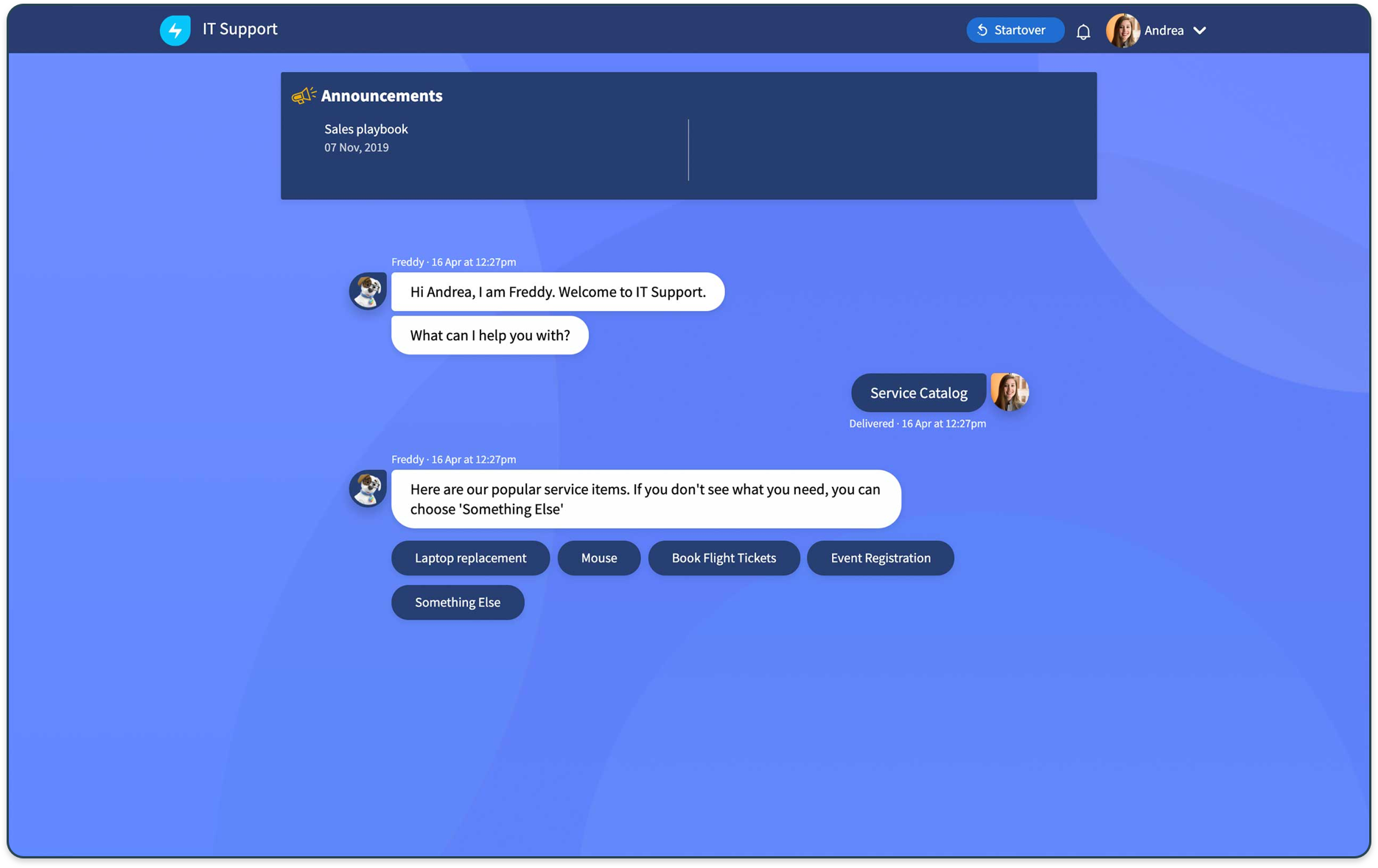 Freshservice - Empower employees with a consumer-grade user experience in the channel of choice, whether MS Teams, Slack, or with the Freshservice chatbot.
Freshservice - Empower employees with a consumer-grade user experience in the channel of choice, whether MS Teams, Slack, or with the Freshservice chatbot. 




Freshservice: its rates
Pro Plan Monthly
€59.00
/month /user
Pro Plan Yearly
€49.00
/month /user
Clients alternatives to Freshservice

Empower your IT team with comprehensive device management, real-time monitoring, and automated patch updates.
See more details See less details
ManageEngine Endpoint Central offers a robust suite for IT monitoring. It provides comprehensive device management, ensuring real-time monitoring and streamlining automated patch updates. These features help maintain system security and optimize IT infrastructure, providing an all-in-one solution suitable for businesses of various sizes.
Read our analysis about ManageEngine Endpoint CentralBenefits of ManageEngine Endpoint Central
Single workflow for both Endpoint Management and Endpoint Security
Industry-leading broad support for multiple OSs and devices
Supports patches for 1000+ third-party software applications
To ManageEngine Endpoint Central product page

ITSM software for streamlined service delivery, incident management, and asset tracking. Automate workflows and improve service quality.
See more details See less details
ManageEngine Servicedesk Plus helps IT teams manage service requests, incidents, and assets from a single platform. It offers customizable workflows, SLA management, a self-service portal, and more. By automating routine tasks and ensuring timely issue resolution, it helps teams improve service quality and reduce downtime.
Read our analysis about ManageEngine Servicedesk PlusBenefits of ManageEngine Servicedesk Plus
ITSM best practices
ITAM
Strong customer focus
To ManageEngine Servicedesk Plus product page

MSP software with automated ticketing, remote monitoring and management, and real-time reporting.
See more details See less details
NinjaOne streamlines your IT services with automated ticketing, remote monitoring and management, and real-time reporting. Reduce downtime and improve customer satisfaction with our MSP software.
Read our analysis about NinjaOne (ex-NinjaRMM)Benefits of NinjaOne (ex-NinjaRMM)
Unified, integrated software
Easy to use, modern, and fast
Repetitive task automation
To NinjaOne (ex-NinjaRMM) product page
Appvizer Community Reviews (0) The reviews left on Appvizer are verified by our team to ensure the authenticity of their submitters.
Write a review No reviews, be the first to submit yours.
